在使用 RSA 公钥加密请求的参数之前，我们先把围绕着 RSA 算法相关的概念、应用和工具做一个简单的整理。

什么是 RSA 算法

RSA 是1977年公布的一种公钥密码算法。由它的三位创始人 Ron Rivest，Adi Shamir 和 Leonard Adleman 的姓氏的首字母命名。那么，为什么说 RSA 是一种公钥密码算法呢？我们通过它的加密解密过程来解释这个事情。

在 RSA 中，加密的对象是数字，也就是说，任何要加密的内容，都要通过某种形式变成数字之后，才能应用 RSA。因此，RSA 的加密过程可以用下面这个公式表达：

encrypted = (data) ^ E mod N

也就是说，计算要加密的数字的 E 次幂再对 N 取模，得到的就是加密后的结果。其中，E 和 N 当然也是数字。至于要怎么得到这些数字，我们稍后再说。接下来，解密的公式是这样的：

data = (encrypted) ^ D mod N

计算加密结果的 D 次幂再对 N 取模，就可以还原出原始数据（当然，这里 D 也是一个数字）。通过这个过程，可能你已经发现了，RSA 加密和解密算法执行的计算是一样的，只是参与计算的数值不同，是不是很神奇？至于为什么可以这样，这背后牵扯到大量数论的知识，显然这已经超出我们要讨论的范畴。因此，只要理解这个过程就好了。

接下来要解决的问题，就是如何找到上面公式中的 E D 和 N 了。同样，我们不去研究具体的原理，而只是注重获取到这些值的过程。

首先，准备两个很大的质数 p 和 q，如果这两个值小了，就会容易被破解。一会儿我们就会看到 RSA 中的整数究竟大到了什么规模。这里，为了计算方便和演示，我们就取两个较小的质数，让 p 等于 5，q 等于 7。

其次，计算 p x q 的值，这个值就是公式中的 N。在我们的例子中，N 等于 35。

第三，为了计算 E，我们要先计算 p-1 和 q-1 的最小公倍数，把这个数计做 L。在我们的例子中，也就是计算 4 和 6 的最小公倍数，显然，L 等于 12。

第四，在 1 和 L 之间，找到一个和 L 的最大公约数为 1 的值，这个值就是公式中的 E。当然，这个值并不唯一。在我们的例子中，就可以是 5 7 11 都满足条件。这里，我们选择 5。这样，公式中的 E 和 N 就都有了。

最后，来算 D。D 的值必须满足这样的条件：D x E mod L = 1。在我们的例子中，也就是 D x 5 mod 12 = 1。显然，D 也不是唯一的。这里我们选择一个满足条件的即可，例如：D 等于 17。

这样，就得到了执行 RSA 算法需要 N E D。接下来，我们用这些值，试一下 RSA 加密和解密。出于 RSA 算法的特性，加密的值必须小于 N，因为解密的时候，计算原始数据的值要对 N 取模。

在演示的例子中，也就是只能加密小于 35 的值。我们就用 11 来举例，按照加密的公式，RSA 的加密结果是 16：

11 ^ 5 mod 35 = 16

再来对 16 解密：

16 ^ 17 mod 35 = 11

就还原回了原始的数字 11，这就是一个最基础的 RSA 加密解密的流程演示了。通过这个例子我们就明白了，只要持有 E 和 N，就能用它们进行加密，而这一对数字，就是常说的公钥。经过这一对公钥加密的内容，只有持有 D 和 N 的人才能解密，于是 D 和 N 这一对数据，就是与之对应的私钥。由于加密和解密使用的“钥匙”不同，因此，RSA 也叫做非对称加密算法。

真实的 RSA 密钥对

对 RSA 算法有了一个感性的了解之后，我们来看看真实的 RSA 密钥对。为此，打开终端，先执行下面的命令创建私钥：

openssl genrsa -out private.pem 2048

其中，2048 指的是私钥的长度，默认值就是2048，并且，这个值不能小于512。执行后，当前目录中就会生成一个叫做 private.pem 的文件，这就是私钥了。然后，再执行下面的命令从 private.pem 中提取出公钥：

openssl rsa -in private.pem -outform PEM -pubout -out public.pem

这样，我们就得到了一对真实的 RSA 密钥对。分别打开这两个 pem 文件看一下，private.pem 是类似这样的：

-----BEGIN RSA PRIVATE KEY-----
MIIEpAIBAAKCAQEAy8N3l3JkkOnLRmDtr5oHQArUA+QUn+BhhUbgjkKD7ElxmABz
J4sJfcD+OUbJqJ/p3v4BjRZuI1ErgQdbtSLiXE6UpGU5RZKn4vLVsRrvDwEv8aC3
uOqDzAkTwVCdskynL9Yz1NIP0dTGiYhQEy8v5TurwP4BfZH6q/OdtTx8KdtlGsQH
yj8yykZgC1eeTT8rujdJSMKyUz2XaOjgAvUqOtW12Q5VqimPBeXnY0wraxZO3w2F
8NCaGOhLklbKdQHEFyZK8TEj02KQIdkwKtZS4wc/3IPlr6fZ28rYzg575X5LysBM
5C+7WmOoz9nszdGFpdupWS9JjtipgvSGZRTB6QIDAQABAoIBAQCHIRwAXaZ/y+w4
wjMej2FbgVLVOb7Lv/wsbLKi5U2jt5kTmsjDYptqwEBYL6+wmkx4y66vqD5mQYA+
U2joGThQyvQcidyPXRDlmvFIQHplUv4+mbz9btj0yNhHDXVnNxpwyPcanixLlXYM
409nSZXTydy/YjQO2G6K9kaSWIhnIJ9faZOkev3LHRcXKqpMbrHRuTCxUiAWv+Ad
aKd4w9n76LUj0rC/15kbj44vHO62rPuR6hV64iol2vEBkkIYYSNk3/kCpOWw9okO
PA9Afdm/JdD1nzny+EP2tL3pkAz5hwNhrJPjw90DTju9akk2IIOiijQ+sF2FdLmQ
rIG/1TIBAoGBAOVP9MnavlpaZGB1V+pgHzNi31SSiGe/WOWS9gIHM/D2A4k0Cp3J
hpQDy2qa+dNLpzrFmpK57vQiVY6AfnOdIvWQtx3fJUzDRRSQrIy490f3zOlUXNG3
/PgmxJmGTd3u96UDH8bPEdJwoPJU4zDEgI9Zq2HcymEBOUNfBC3DO3xhAoGBAON6
UfmDvoOnILFHsifTxIFqX/DJM3xYQtmxbMcA1gwLlnQN5X+HVtCIdIDFqhv5bp4d
BUEl2VxP3Lzs4estqOajuV6mjPOMfcmSiMmuRlHv4jtSifcas3/adVg0sSJpnuDg
b9N9UOQNfrjQnnXSnxdV338SiCd2LZ4o5eH6XHKJAoGAPHnt0R6DfUjBmD7aRNG8
6Mx2odNTbikkxMcRYk+L/0yiehjjg+GWQIsPprngkT0uiW176p5myrQTZFW3A765
bZIQ+SvUpn4JRfcxypstfCl6PT8mi5i+eqOeze6BsrpHTZmZU9FgneNeTwrcMAxi
62t2q4STSyoLdB0m+Pq4QYECgYEAnOYasoInHsFgsEZmYEgVaroHUJpGU8bA3Uwe
Xih6erZnYMbQ+6RKwezMhqFP0pm5rX8Qx72mbaB7/SdaMA8/R024Jsuzvqyxeh4D
ETCOOie+H/KvTGvzUQVKGLvHTZgSSMMk/neaGqIgPLNQCK5sovjM/eW3WZiOoF9P
KA26RBkCgYASiNdFPcyqlkSe7WtbP97xWozQwi2PbJZsKimkMvVmI6JGTT97JaTT
9b8io2abPozDRrh+tQZunac1dqrDBg1Mt0bpRSuY6aIRsU4VdR5JegM2SgeNckz6
EKNmwzIZy79Q5+Ls9JSIlcPEZaUGiQLP7FUphdtL5W/3k9ObYLcdNw==
-----END RSA PRIVATE KEY-----

而 public.pem 的内容是类似这样的：

-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAy8N3l3JkkOnLRmDtr5oH
QArUA+QUn+BhhUbgjkKD7ElxmABzJ4sJfcD+OUbJqJ/p3v4BjRZuI1ErgQdbtSLi
XE6UpGU5RZKn4vLVsRrvDwEv8aC3uOqDzAkTwVCdskynL9Yz1NIP0dTGiYhQEy8v
5TurwP4BfZH6q/OdtTx8KdtlGsQHyj8yykZgC1eeTT8rujdJSMKyUz2XaOjgAvUq
OtW12Q5VqimPBeXnY0wraxZO3w2F8NCaGOhLklbKdQHEFyZK8TEj02KQIdkwKtZS
4wc/3IPlr6fZ28rYzg575X5LysBM5C+7WmOoz9nszdGFpdupWS9JjtipgvSGZRTB
6QIDAQAB
-----END PUBLIC KEY-----

为了了解这两个文件的内容，我们得从它们的格式，也就是 PEM 格式说起。大家可以在这里找到 PEM 格式的详细说明。简单来说，这种格式的文件用 -----BEGIN 开头，-----END 结尾。开头和结尾后面跟着的，是文件内容的说明，例如上面看到的 RSA PRIVATE KEY 或者 PUBLIC KEY，稍后创建证书的时候，还可以在这里看到 CERTIFACTE。

而在开始和结束标记之前的，则是经过 BASE64 编码的文件内容。在我们的例子中，也就是 RSA 的私钥和公钥。但 BASE64 解码的内容是纯二进制格式的，非常不便于观察。如何能从中找到之前说过的 E D 和 N 呢？

ASN.1 编码

实际上，PEM 文件解码后的内容，是通过一种叫做 ASN.1 的编码方式组织起来的，而这种二进制的形式也是一种可用的证书格式，通常用 .der 作为后缀名。我们可以执行下面两条命令在 DER 和 PEM 这两种格式之间转换：

# DER -> PEM
openssl rsa -inform DER -in public.der -out public.pem

# PEM -> DER
openssl rsa -inform PEM -in public.pem -outform DER -out public.der

那究竟 ASN.1 又是如何定义公钥内容的呢？用一张图表示，就是这样的：

可以看到，这是一个递归的定义。整个文件的最外层，是通过：

• TAG：标记数据类型；
• LENGTH：标记数据长度；
• CONTENT：数据内容；

这三部分组成的。然而，在 CONTENT 内部，数据依旧通过 T L C 这三部分定义。因此，我们只要用这种方式，不断根据 T L C 的值去解析文件直至结束，就可以分析出证书的内容了。

找到存储在公钥中的 E 和 N

好在，互联网上有很多在线解析公钥的服务可以帮助我们观察 ASN.1 格式。这里，我们就用 asn1js 来观察下之前生成的公钥。

不要通过这种方式浏览任何部署在生产环境的证书和密钥对。

把之前生成的 public.pem 的内容粘贴到输入框，点击 decode 按钮，就会看到类似这样的结果：

图中，左边的部分，是公钥文件的内容层次结构，右边的部分，是 ASN.1 编码的二进制结果。其中蓝色的字节表示 TAG，绿色的字节表示 LENGTH，黑色的字节表示 CONTENT。接下来，我们就边分析这个公钥，边讲一下如何理解这份数据。

首先，读入的 TAG 是 0x30，它表示接下来的内容，是由一系列 T L C 标记的数据。

其次，读入的 LENGTH 是绿色的 0x82 0x01 0x22。实际上，ASN.1 编码的 LENGTH 有两种格式，一种是单子节的短格式，这种格式，LENGTH 字节的最高位是 0，因此它只能标记长度小于 127 字节的数据；另一种是长格式，它的第一个字节的最高位是 1，剩下的 7 个 bit 用于表示后面还有多少个表示长度的字节。在我们的例子中，这个字节是 0x82，显然这是一个长格式，后面还有两个表示长度的字节。然后，把后面这两个字节组合起来，变成 0x122，就是后面 CONTENT 部分的长度了。因此，整个公钥的长度，就是 1 + 3 + 290，也就是 294 字节。

第三，继续读 CONTENT 的部分。第一个字节还是 0x30 表示之后还有 TLC 这样的结构化数据。第二个字节是 0x0D，这是一个短格式的长度，表示后面的有 13 字节的 CONTENT。

第四，这个 13 字节的 CONTENT 的第一字节是 0x06，这个 TAG 的含义是标识符，这个标识符用于区分不同的算法，它的长度是 9 字节。接下来的 9 字节数据可以表示成 1.2.840.113549.1.1.1 这样一串标识符。至于是如何得到这个结果的，大家感兴趣可以参考这篇博客，我们就不展开说了。

第五，接下来的一个字节是 0x05，这个 TAG 表示 NULL，它后面的 LENGTH 当然就是 0。对于 NULL TAG，是没有 CONTENT 部分的。

第六，下一个字节是 0x03，这个 TAG 表示接下来的内容是二进制比特串。它的 LENGTH 是 0x82 0x01 0x0F，这个长格式表达的 CONTENT 长度是 271 字节。接下来这个二进制比特串由两部分组成，因此，它的 CONTENT 部分是0。需要我们继续往后解析。

第七，下一个 TAG 值又是 0x30 表示一个序列，这个序列的长度是 0x10A；

第八，就是这个公钥中最关键的部分了。它的 TAG 是 0x02，表示一个整数，这个整数的长度是 0x101。但从上面的图中可以看到，这部分的首字节为0，也就是说实际的整数只有 0x100 字节，也就是 256 字节，换成比特数就是 2048。看到这，你想起来什么了么？没错，这正是我们通过 openssl 生成证书的时候，指定的长度，而这 2048 比特构成的整数，正是 RSA 算法中用到的 N。

最后一个 TAG 仍旧是 0x02 表示一个整数， LENGTH 是 3，CONTENT 是 0x10001，这个值就是 RSA 算法中用到的 E。也就是说，用这个公钥加密，要计算原始数据的 65537 次幂，然后把结果对一个 2048 比特的整数求余数。光想想，就知道这是一个多么大的算数了。

至此，我们就解析了一个真实的 RSA 公钥，它就是一个用特定格式存储 E 和 N 的文件。

找到存储在私钥中的 D 和 N

有了分析公钥的经验之后，我们再来看看私钥。为什么对于非对称加密算法都说公钥可以任意发布，但是私钥一定要握在自己手里不能泄漏呢？分析了私钥文件的格式之后，你就明白了。同样，我们把之前生成的私钥也导入 asn1js，看到结果，是类似这样的：

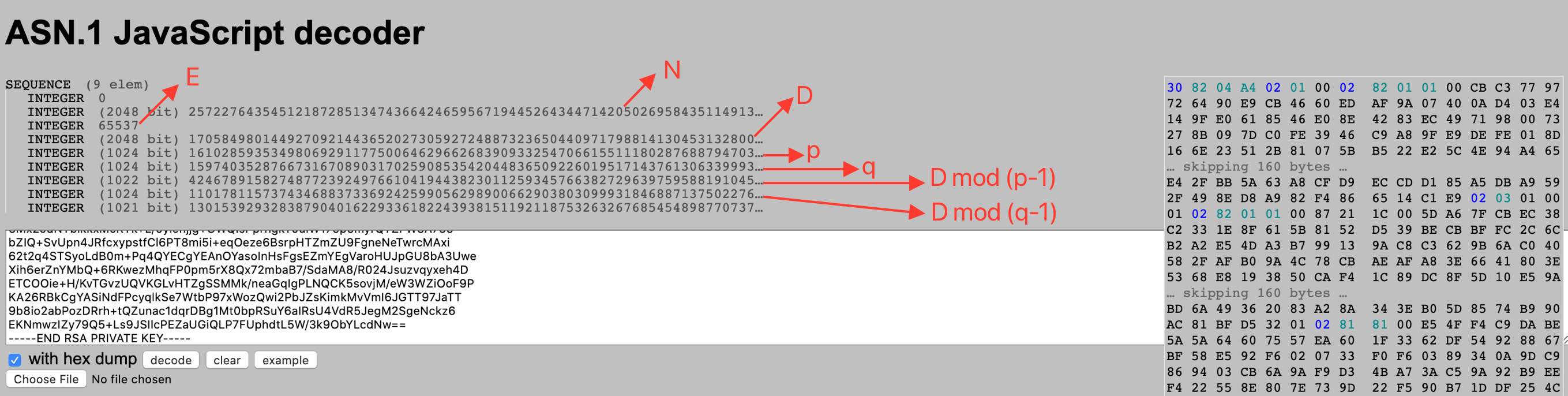
很明显，从图左侧的内容结构来说，私钥要比公钥长很多。这次，我们就不再逐字节分析私钥的二进制格式了，因为这个过程和分析公钥是完全相同的，大家可以自己练习。我们主要通过左侧的内容结构，来看看私钥里究竟有什么东西。

首先标记的 2048 比特，是 N，这部分和公钥是一样的。N 后面的 65537 是 E。也就是说，私钥中是包含完整公钥信息的。

其次，E 后面的 2048 比特，就是解密公式中的 D。

第三，D 后面的两个 1024 比特，分别是生成密钥对时使用的 p 和 q；

第四，q 后面的，则分别是 D mod (p-1) 和 D mod (q-1) 的值；

也就是说，之前我们演示 RSA 加密解密过程中用到的所有信息，都保存在了私钥里。看到这，你也就能明白为什么公钥可以自由分发，但私钥必须要保密了吧。

带有密码的私钥

正是由于私钥包含了和加密解密相关的所有信息，为了进一步提高它的安全性，我们还可以创建带有密码的私钥。为此，在生成密钥的时候，可以执行下面这条命令：

openssl genrsa -des3 -out private_des3.pem 2048

其中，-des3 就是加密私钥信息使用的算法。除了它之外，我们还可以使用 des / aes-128 / aes-192 / aes-256 等加密算法。执行之后，openssl 就会要求我们输入私钥密码。要注意的是，一旦这样做了，私钥密码和私钥就同等重要了，我们必须同时保管好它们。

查看下生成的私钥，就会变成类似下面这样的内容：

-----BEGIN RSA PRIVATE KEY-----
Proc-Type: 4,ENCRYPTED
DEK-Info: DES-EDE3-CBC,7D15AED8DD5B98F1

yqWHE9u/Ydr6441NmyWnaHsgUCIy2eSM573IAFcosR1QHYLQFw5kRMOsM2Tix9UM
l9OxT43Eqmcr0VszcqhGbXXFc6WzVdTlOYE+5dh72BEF9C2rdwG5dzt2iNHn8Z77
dx53Rf7bk4WaBKDRTvbnq3f38CiaCZjQqPbGcFBsT70wQHGiGqBG3iF6cLMKQz7E
em8SKMaAk6VY8qw+xCeU32bvCnz3fDhg2PE2ihKO/NxYuk62JIzjgq51UnjkYxno
S08H6Z5sI91kT8w5ORXstA9vPiH/PMW5REVbeaxvOJlc+ecxVOrWpd9vVt2lDtGS
...
-----END RSA PRIVATE KEY-----

PEM 格式会明确告诉我们这是一个经过 DEC3 加密的私钥，因此也就不能直接对其中的内容进行 base64 解码了。

What's next?

以上，就是通过 RSA 进行加密和解密的内容。看过了它的工作方式以及密钥格式之后，无论是 RSA 算法本身，还是所谓的密钥对，你应该一点儿都不感到陌生了。为了通信安全，我们给需要的对象发放公钥用于加密数据，自己则持有私钥用于解密。然而，加解密并不是 RSA 唯一的用法。下一节，我们来看如何通过 RSA 完成数字签名和验签。

Discuss It

参与视频讨论