这一节，我们完成两个工作。首先，实现AES加密的基本流程；其次，了解AES加密的几种常用工作模式。

实现AES加密

实际上，有了前面几节的内容准备，实现AES加密就非常简单了。直接来看代码：

void Cipher(state_t* state, const uint8_t* RoundKey)
{
  uint8_t round = 0;
  AddRoundKey(0, state, RoundKey);

  for (round = 1; round < Nr; ++round)
  {
    SubBytes(state);
    ShiftRows(state);
    MixColumns(state);
    AddRoundKey(round, state, RoundKey);
  }

  // The last round is given below.
  SubBytes(state);
  ShiftRows(state);
  AddRoundKey(Nr, state, RoundKey);
}

其中：

• state指向要加密的钥匙数据；
• RoundKey指向扩展好的密钥；

整体的执行流程，就是在前面几节介绍的过程。在这段代码里，我们能更清楚地看到加密过程中的“轮”究竟是如何计算的。例如，AES-128，我们之前说过，它要执行10轮加密。但实际的执行过程是这样的：

• 第0轮，把原始数据和原始密钥进行异或；
• 第1-9轮，执行SubBytes -> ShiftRows -> MixColumns -> AddRoundKey的完整流程；
• 第10轮，不执行MixColumns；

因此实际执行的，是11轮操作。而对于解密算法，就是把Cipher的执行倒过来：

void InvCipher(state_t* state, const uint8_t* RoundKey)
{
  uint8_t round = 0;
  AddRoundKey(Nr, state, RoundKey);

  for (round = (Nr - 1); round > 0; --round)
  {
    InvShiftRows(state);
    InvSubBytes(state);
    AddRoundKey(round, state, RoundKey);
    InvMixColumns(state);
  }

  InvShiftRows(state);
  InvSubBytes(state);
  AddRoundKey(0, state, RoundKey);
}

其中的InvShiftRows / InvSubBytes / InvMixColumns分别是对应算法的逆运算。大家可以到GitHub去看代码，理解它们并没有难度，我们就不重复了。至此，关于AES加密算法的执行流程，就说完了。不过，只能对定长数据加密始终都是一个缺陷。因此也就有了接下来关于AES加密工作模式的话题。简单来说，就是把不定长的数据，切分成若干定长的数据，再进行加密和解密。

分组密码的工作模式

当我们搜索AES加密应用的时候，经常能看到诸如AES-256-ECB / AES-256-CBC这样的名字。它们执行的都是AES加密算法，其中的ECB / CBC指的就是它们的工作模式。

ECB

我们先从最简单也最不安全的ECB模式说起。所谓ECB模式，就是直接把原始要加密的数据按照定长分组，然后每一个分组用同样的Key执行加密：

很好理解对不对？但这种模式最大的问题就在于一旦原始数据的存储格式暴露了，攻击者可以无需AES密钥就对加密数据进行攻击。来看个经典的例子，假设银行账号A向账户B转账的信息是通过下面的格式存储的：

账户A: uJb17CO3LSj+SFPSTSRpUg==
账户B: 3HFW8zvoG9f4kB80B+6hrg==
转账金额: T48Km+rTBItaZim/kRvgww==

对于这组加密的数据，出于ECB模式的特性，任意改变这三行的顺序，都不会影响解密结果，因为它们的加密解密过程是完全独立的。于是，攻击者只要尝试把数据的前两行换位，这个转账的顺序就变成了账户B向账户A转账，从而达成了在不知道AES密钥的情况下攻击原始数据。因此，除非是为了向既有系统兼容，现如今ECB这种工作模式已经不被使用了。

数据的padding

不过看到这，你可能会想了，怎么那么巧原始数据能分到AES加密数据块的整数倍呢？实际上当然不可能这么巧了。这就涉及到数据的补全问题。我们常见的补全策略，有三种，分别是：zero padding，PKCS #5 padding和PKCS #7 padding。对于PKCS #5和PKCS #7的“身世”，现在我们不用追求太多，它们涉及到和证书相关的内容，等稍后用到RSA加密算法的时候再说。但现在我们可以从编程的角度来理解下这三种填充方法的实现，因为这涉及到AES加密函数的用法。

首先是zero padding，这种方法最简单，在欠缺的位置都填充0就行了。

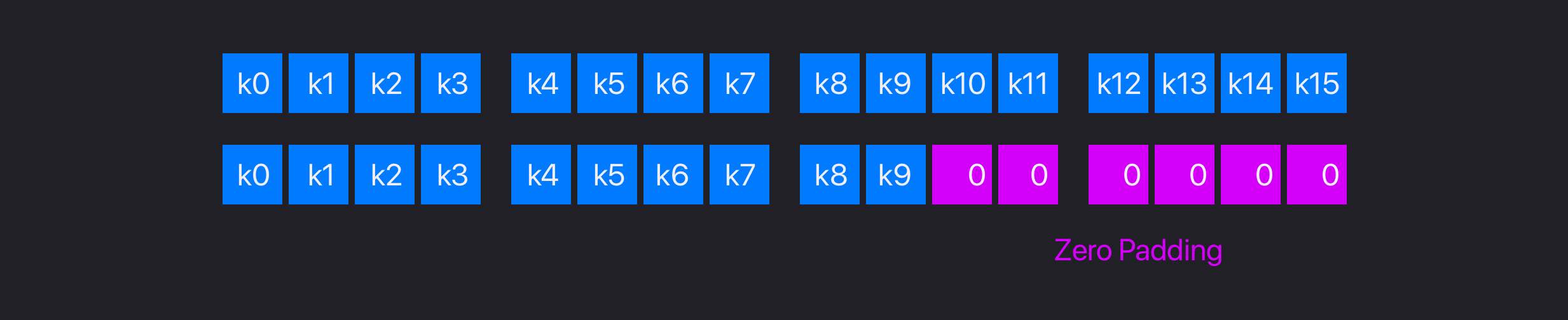
例如，目标字节是16，当前字节数是10，那么就在结尾补上6个0。例如，图中每一个方块表示1字节，我们要求数据的分组是每16字节分组，对于第二行的情况，就会在末尾补充上6字节的0。这种方法的缺点就是，在解密之后，如果看到结尾包含一个0，我们无法区分究竟是之前填充进来的应该去掉，还是原始数据本身就是0。因此，zero padding通常只用来填充字符串，而不直接用于AES加密算法，因为表示字符串结尾的0本身就是无意义的。

其次，是PKCS #7 padding。它的工作方式是这样的：

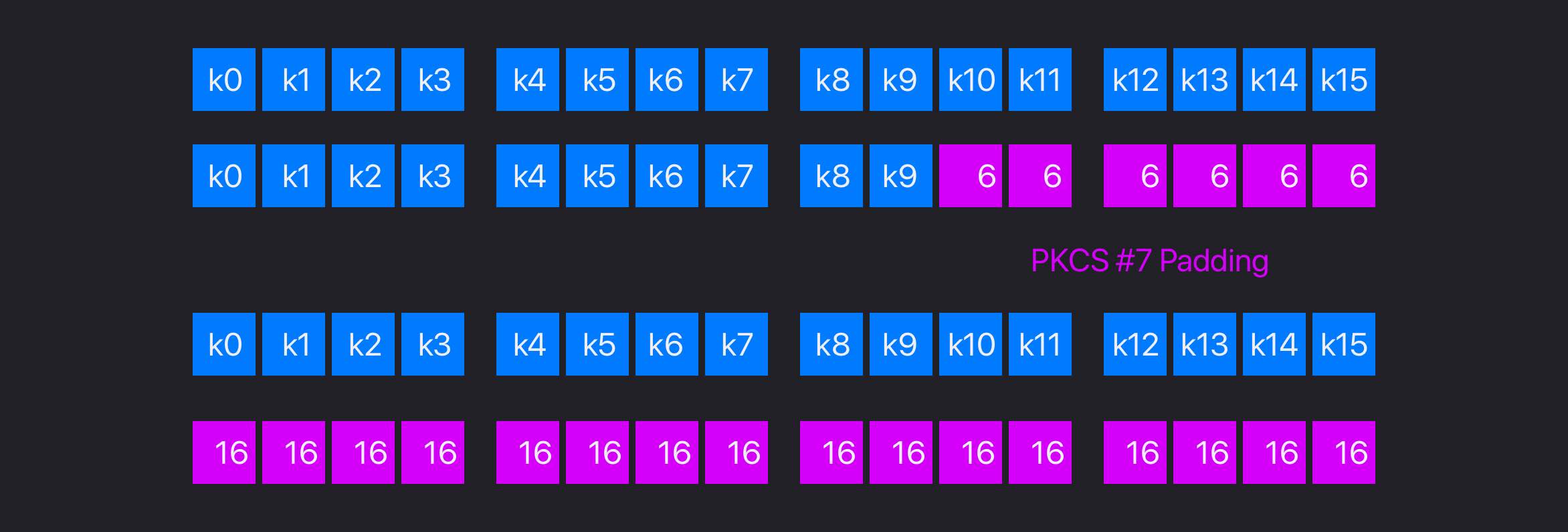
• 假设要求的分块大小是blockSize；
• 如果当前数据大小正好是blockSize，就在当前数据后面再填充上blockSize个值为blockSize的字节；
• 如果当前数据尺寸currSize小于blockSize，就把空缺的部分都填充上blockSize - (currSize % blockSize)；

通过这种方式，我们就知道，解密后得到的数据块，最后一个字节一定是填充的，并且从它的值我们还能知道填充进来的字节数，这样也就能还原回原始的值了。这也是AES加密使用的填充方式。

最后，是PKCS #5 padding。从实现上方式上说，它和PKCS #7是一样的。只不过，它只用于填充以8字节为单位的数据块。因此，PKCS #5并不能用于AES加密算法，只能用于DES加密算法。

CBC

了解了数据padding策略之后，我们继续回到AES的工作模式。既然ECB这种直接分组映射的方式不安全，该怎么办呢？一个思路就是让下一个分组的加密和上一个分组的加密相关，有了这种关联性，移动了加密结果之后，就无法成功解密了。把这个思路具体到CBC上，就是这样的：

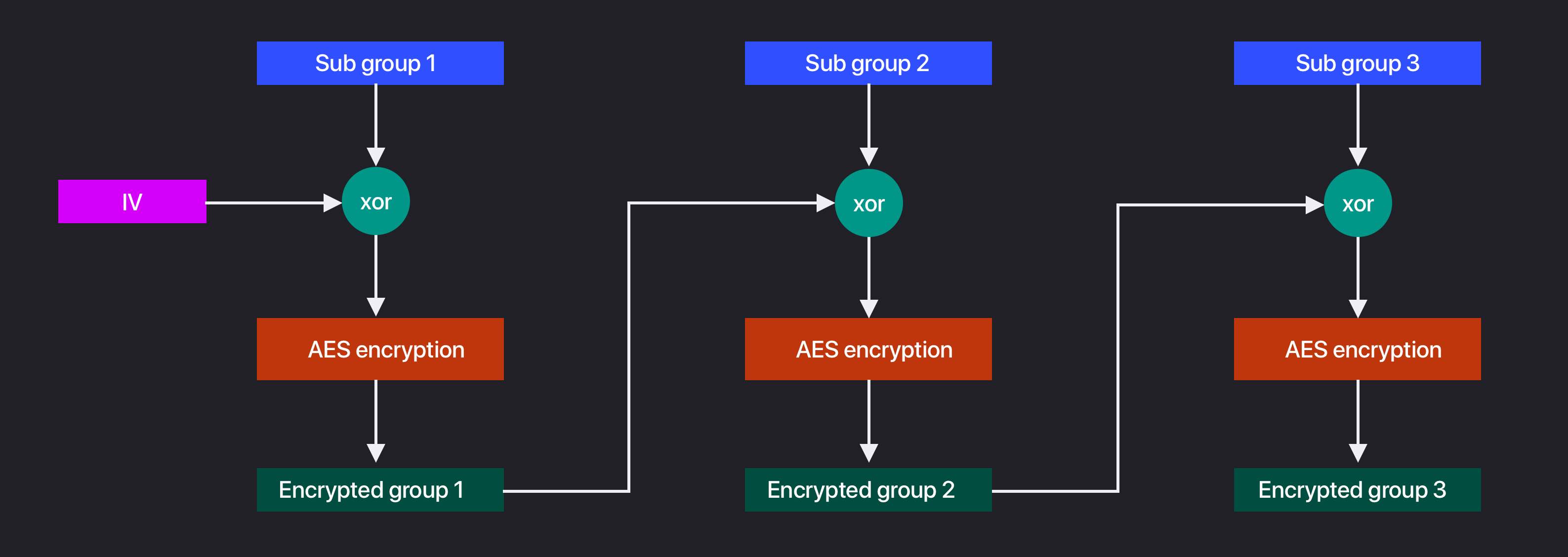
也就是说，第i+1个分组要加密的数据，要先和第i个分组的加密结果异或。这样一来，我们就要为第一个分组的加密创建一个和分组长度相同的随机向量来参与异或（对于AES来说，就是个16字节的数组），这个随机向量，叫做Initial Vector，也叫做IV。

我们不妨来看看它的实现：

void AES_CBC_encrypt_buffer(
  struct AES_ctx *ctx, uint8_t* buf, uint32_t length)
{
  uintptr_t i;
  uint8_t *Iv = ctx->Iv;
  for (i = 0; i < length; i += AES_BLOCKLEN)
  {
    XorWithIv(buf, Iv);
    Cipher((state_t*)buf, ctx->RoundKey);
    Iv = buf;
    buf += AES_BLOCKLEN;
  }
  /* store Iv in ctx for next call */
  memcpy(ctx->Iv, Iv, AES_BLOCKLEN);
}

这里，唯一要解释一下的就是最后一个memcpy的调用，它会保存上一次加密时使用的Iv，也就是说，只要在执行AES加密之初设置了Iv，接下来所有的加密使用Iv就都可以自动生成出来了，我们可以把它看成区块链最原始的形式。

除了ECB和CBC之外，AES还支持CFB / OFB / CTR等工作模式，不过理解了分组加密的想法之后，理解它们并不困难，大家感兴趣的话可以自己去研究，我们就不一一展开了。

What's next?

至此，对于AES加密的执行细节，我们就说的差不多了，从支持这种加密的数学知识，到加密过程的执行细节，再到对不定长数据的扩展方法。下一节，我们就用AES-256-CBC这种方式，来加密APN Provider返回的数据结果。

Discuss It

参与视频讨论