这一节，我们通过一个GitHub上的开源项目tiny-AES-c，来学习AES加密算法的内部实现。参与这个AES加密的成员主要有两个：一个是要加密的原始数据，它必须是固定的16字节长度；把它用C语言表示，就是这样：

typedef uint8_t state_t[4][4];

另一个是加密使用的密钥，它的长度可以是16/24/32字节，分别对应着平时我们说的AES-128/192/256加密算法。我们可以定义一些宏来表示不同AES加密算法使用的密钥长度：

#if defined(AES256) && (AES256 == 1)
    #define AES_KEYLEN 32
#elif defined(AES192) && (AES192 == 1)
    #define AES_KEYLEN 24
#else
    #define AES_KEYLEN 16   // Key length in bytes
#endif

SubBytes

了解了这些基本信息之后，我们就从对原始数据的预处理开始。AES加密算法的第一步，叫做SubBytes。它的目的是对原始数据的每个字节进行混淆。混淆的方法是先计算每一个字节在GF(2^8)的乘法逆元，再把这个逆元按照下面的方式做一次仿射变换（就是乘以一个矩阵再加上一个向量）：

|s0|    |1 0 0 0 1 1 1 1| |b0|   |1|
|s1|    |1 1 0 0 0 1 1 1| |b1|   |1|
|s2|    |1 1 1 0 0 0 1 1| |b2|   |0|
|s3| =  |1 1 1 1 0 0 0 1| |b3| + |0|
|s4|    |1 1 1 1 1 0 0 0| |b4|   |0|
|s5|    |0 1 1 1 1 1 0 0| |b5|   |1|
|s6|    |0 0 1 1 1 1 1 0| |b6|   |1|
|s7|    |0 0 0 1 1 1 1 1| |b7|   |0|

这里的b0-b7表示原始数据中每一个字节的bit，经过上面一番计算，就得到变换之后的值了。由于GF(2^8)中，0没有乘法逆元，我们约定0的乘法逆元就是0。把0带入到上面的公式，不难计算到0混淆之后的值是0x63（这里的乘法和加法要使用GF(2)中的计算规则）。

接下来，我们按照这样的方法，就可以计算出256个值，每个值都对应一个字节的值混淆之后的结果。在很多AES的实现里，为了效率，这些值都是硬编码出来的：

static const uint8_t sbox[256] = {
//0     1     2     3     4     5     6     7     8     9     ...
  0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, ...
  0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, ...
  0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, ...
  ...
};

这里，受篇幅限制，我们只列出了前9列和前3行，实际上，sbox是一个16x16的方针，sbox是Substitution-box的缩写，也就是“替换盒子”。

理解了sbox之后，就不难想到，在解密的时候，还应该有一个盒子用于还原混淆后的结果。这个盒子，叫做Reverse Substitution-box。它的计算方法和加密混淆时是一样的，只是仿射变换时使用的矩阵和向量不同罢了：

|b0|    |0 0 1 0 0 1 0 1| |s0|   |1|
|b1|    |1 0 0 1 0 0 1 0| |s1|   |0|
|b2|    |0 1 0 0 1 0 0 1| |s2|   |1|
|b3| =  |1 0 1 0 0 1 0 0| |s3| + |0|
|b4|    |0 1 0 1 0 0 1 0| |s4|   |0|
|b5|    |0 0 1 0 1 0 0 1| |s5|   |0|
|b6|    |1 0 0 1 0 1 0 0| |s6|   |0|
|b7|    |0 1 0 0 1 0 1 0| |s7|   |0|

当然，我们只要知道这种方法就好了，实际编码的时候，这个“逆替换盒子”，也是硬编码实现的：

static const uint8_t rsbox[256] = {
//0     1     2     3     4     5     6     7     8     9     ...
  0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, ...
  0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, ...
  0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, ...
  ...
};

于是，加密和解密的查表过程，就可以写成这样：

#define getSBoxValue(num) (sbox[(num)])
#define getSBoxInvert(num) (rsbox[(num)])

ShiftRows

看到这里，不难理解SubBytes是bit级别的混淆。接下来，AES还在byte级别进行了混淆，这一步叫做ShiftRows。它的操作用一张图表示就直观了：

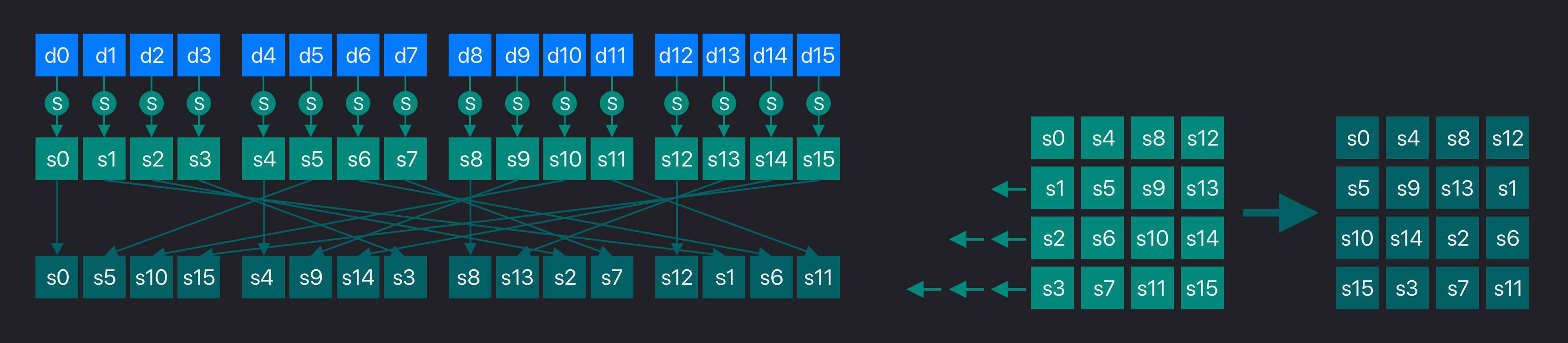
图中的每一个方块，都表示一个字节。其中d0-d15表示原始数据序列。经过第一轮SubBytes变换之后，变成了s0-s15。所谓ShiftRows，就是把s0-s15放到箭头指定的位置。左边的线条看着可能有点乱，但如果把**s0-s15每四个字节一列**变成一个方阵，计算方法就清楚了。所谓的ShiftRows就是把这个方阵的每一行，向左循移动：第0行保持不动，第1行向左移动1个字节，第2行向左移动2个字节，第3行向左移动3个字节。

这个过程实现出来就是这样的，它的输入参数是SubBytes之后的16字节数据：

static void ShiftRows(state_t* state)
{
  uint8_t temp;

  // Rotate first row 1 columns to left
  temp           = (*state)[0][1];
  (*state)[0][1] = (*state)[1][1];
  (*state)[1][1] = (*state)[2][1];
  (*state)[2][1] = (*state)[3][1];
  (*state)[3][1] = temp;

  // Rotate second row 2 columns to left
  temp           = (*state)[0][2];
  (*state)[0][2] = (*state)[2][2];
  (*state)[2][2] = temp;

  temp           = (*state)[1][2];
  (*state)[1][2] = (*state)[3][2];
  (*state)[3][2] = temp;

  // Rotate third row 3 columns to left
  temp           = (*state)[0][3];
  (*state)[0][3] = (*state)[3][3];
  (*state)[3][3] = (*state)[2][3];
  (*state)[2][3] = (*state)[1][3];
  (*state)[1][3] = temp;
}

而对于解密的过程，则是把方阵的每一行按照上面的规则向右平移就好了。

MixColumn

ShiftRows完成后，我们就得到了一个进一步被打乱次序的字节序列。接下来，AES要继续以每4个字节为单位进行混淆，这一步叫做MixColumn。

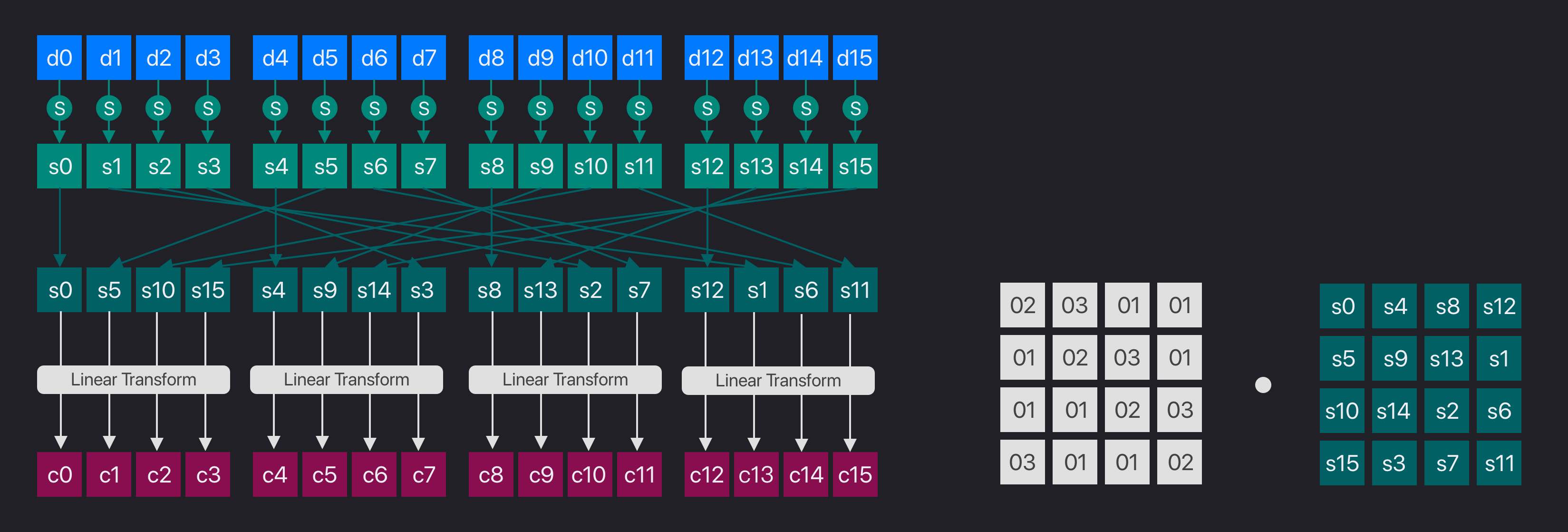
如图中所示，我们用下面这个方阵和ShiftRows之后的结果相乘：

|02 03 01 01|
|01 02 03 01|
|01 01 02 03|
|03 01 01 02|

得到的新方阵，就是MixColumn的结果。不过，这里的矩阵运算，要使用GF(2^8)中的加法和乘法。例如，假设ShiftRows之后的方阵是这样的（这里只是为了演示方便，实际不可能是这种结果的）：

|11 11 11 11|
|11 11 11 11|
|11 11 11 11|
|11 11 11 11|

00010001 对于十六进制数字0x11，它对应的多项式是x^4+1，和它进行计算的矩阵中的01 / 02 / 03对应的矩阵分别是1 / x / x+1，于是：

01 * 11 = 1 * (x^4 + 1) = x^4 + 1
02 * 11 = x * (x^4 + 1) = x^5 + x
03 * 11 = (x + 1)(x^4 + 1) = x^5 + 1

因此，相乘之后这个方阵的结果就是：

(01 + 01 + 02 + 03) * 11
= (1 + 1 + x + x + 1) * (x^4 + 1)
= x^4 + 1

由于这个结果的最高次幂没有超过x^7，我们就不用对P(x)取模了。当然，这个运算的结果并不重要，大家理解这个以4字节为单位的混淆过程就好了。接下来的问题就是，如何通过编程实现呢？

为了理解这个方法，我们先手动算几个值。现在，假设state_t中已经是ShiftRows操作完成之后的结果了。按照之前的说明：c0 = 2s0 + 3s5 + s10 + s15。

但别忘了，我们执行的是多项式运算，因此要把2和3替换成对应的多项式：

xs0 + (x+1)s5 + s10 + s15

把它展开，就是：

x(s0 + s5) + s5 + s10 + s15

这里的s0 / s5 / s10 / s15对应着state_t[0][0] / [0][1] / [0][2] / [03]，于是，这个式子还能写成这样：

c0 = x(state_t[0][0] + state_t[0][1])
     + state_t[0][1] + state_t[0][2] + state_t[0][3]

接下来，算c1，用同样的方式，不难得到这样的结果：

c1 = x(state_t[0][1] + state_t[0][2])
     + state_t[0][0] + state_t[0][2] + state_t[0][3]

最后，我们把c0 - c3的结果罗列在一起：

c0 = x(state_t[0][0] + state_t[0][1])
     + state_t[0][1] + state_t[0][2] + state_t[0][3]

c1 = x(state_t[0][1] + state_t[0][2])
     + state_t[0][0] + state_t[0][2] + state_t[0][3]

c2 = x(state_t[0][2] + state_t[0][3])
     + state_t[0][0] + state_t[0][1] + state_t[0][3]

c3 = x(state_t[0][3] + state_t[0][0])
     + state_t[0][0] + state_t[0][1] + state_t[0][2]

发现其中的规律了么？在每一个结果的第二行，其实都差了一个元素state_t[0][i]，只要补上这个值，第二行的计算就相同了，于是c0还可以写成这样（注意这里执行的是GF(2)加法，1+1=0）：

c0 = x(state_t[0][0] + state_t[0][1])
     + state_t[0][1] + state_t[0][2] + state_t[0][3] + state_t[0][0]
     + state_t[0][0]

接下来，来看第一行的部分。还是用c0举例，在乘以x之后，结果有两种情况：

• 第一种情况是最高次幂没有超过x^7，这时的结果就是相乘之后的结果，对应的计算方法，就是把state_t[0][0] + state_t[0][1]向左移动一个bit（这里执行的是GF(2)乘法）；
• 第二种情况是最高次幂变成了x^8，这时，我们就要把这个多项式对P(x)取模，这个操作是有固定方法的，就是把结果左移1bit之后和0x1B进行xor操作；

于是，这个乘以x的部分，可以实现成下面就这样：

uint8_t xtime(uint8_t x) {
  return (x<<1) ^ (((x>>7) & 1) * 0x1b);
}

至此，用于计算MixColumn的细节就都说完了，把它们组合成一个函数，就是这样的：

void MixColumns(state_t* state)
{
  uint8_t i;
  uint8_t Tmp, Tm, t;

  for (i = 0; i < 4; ++i)
  {
    t   = (*state)[i][0];
    Tmp = (*state)[i][0] ^ (*state)[i][1] ^ (*state)[i][2] ^ (*state)[i][3] ;

    Tm  = (*state)[i][0] ^ (*state)[i][1] ;
    Tm = xtime(Tm);
    (*state)[i][0] ^= Tm ^ Tmp ;

    Tm  = (*state)[i][1] ^ (*state)[i][2] ;
    Tm = xtime(Tm);
    (*state)[i][1] ^= Tm ^ Tmp ;

    Tm  = (*state)[i][2] ^ (*state)[i][3] ;
    Tm = xtime(Tm);
    (*state)[i][2] ^= Tm ^ Tmp ;

    Tm  = (*state)[i][3] ^ t ;
    Tm = xtime(Tm);
    (*state)[i][3] ^= Tm ^ Tmp ;
  }
}

理解了上面的计算过程，这段像“天书”一样的代码就不难理解了。要再次强调的是，我们执行的是GF(2)中的加法和乘法，也就是说，加法是xor运算，乘法是and运算。

而解密时MixColumns执行的操作，和加密是一样的，只不过方阵相乘的时候，使用的常数方阵值不一样罢了

|0E 0B 0D 09|
|09 0E 0B 0D|
|0D 09 0E 0B|
|0B 0D 09 0E|

What's next?

当执行完了MixColumns的四轮操作之后，对原始数据的混淆工作，就结束了。接下来要做的事情，就是根据使用的密钥长度，对混淆过的数据进行不同轮数的加密。下一节，我们就来实现这个过程。

Discuss It

参与视频讨论